Package de.lmu.ifi.dbs.elki.algorithm.clustering.kmeans

K-means clustering and variations.

See: Description

Interface Summary

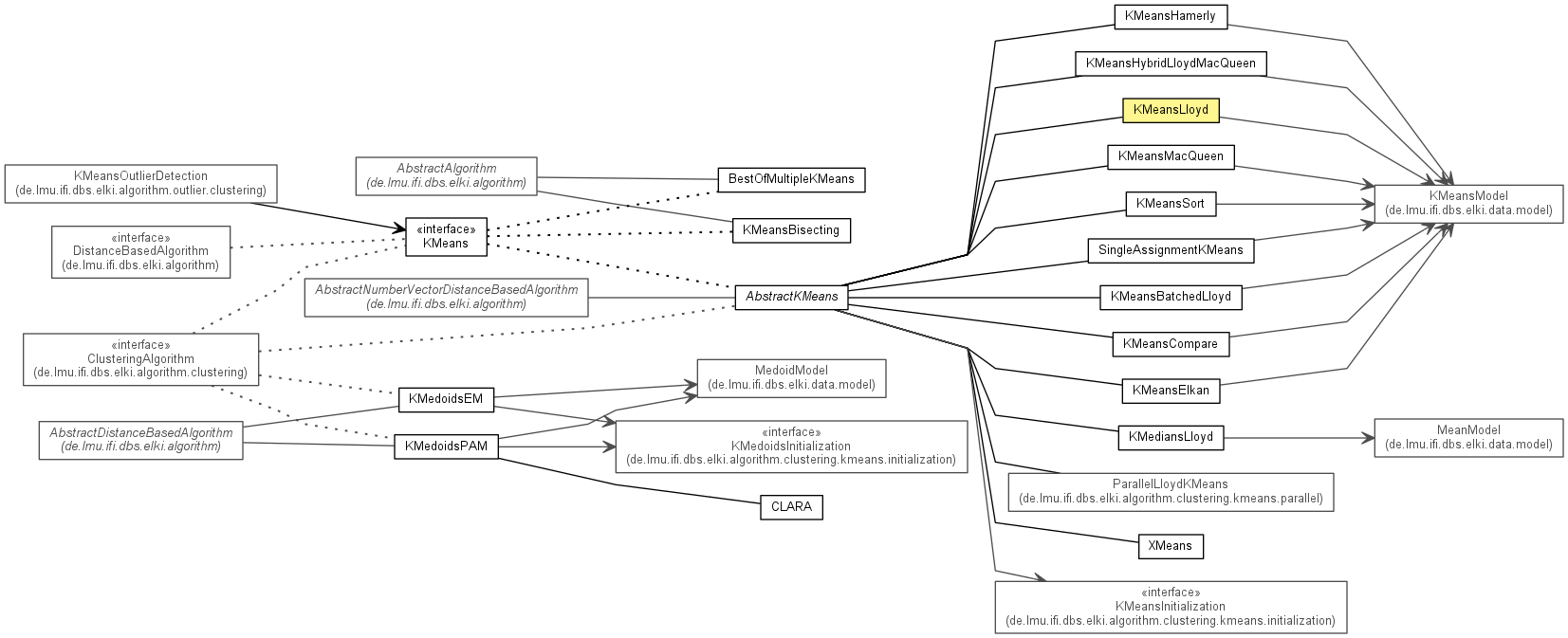
Interface	Description
KMeans<V extends NumberVector,M extends Model>	Some constants and options shared among kmeans family algorithms.

Class Summary

Class	Description
AbstractKMeans<V extends NumberVector,M extends Model>	Abstract base class for k-means implementations.
AbstractKMeans.Parameterizer<V extends NumberVector>	Parameterization class.
BestOfMultipleKMeans<V extends NumberVector,M extends MeanModel>	Run K-Means multiple times, and keep the best run.
BestOfMultipleKMeans.Parameterizer<V extends NumberVector,M extends MeanModel>	Parameterization class.
CLARA<V>	Clustering Large Applications (CLARA) is a clustering method for large data sets based on PAM, partitioning around medoids (KMedoidsPAM) based on sampling.
CLARA.Parameterizer<V>	Parameterization class.
KMeansBatchedLloyd<V extends NumberVector>	An algorithm for k-means, using Lloyd-style bulk iterations.
KMeansBatchedLloyd.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansBisecting<V extends NumberVector,M extends MeanModel>	The bisecting k-means algorithm works by starting with an initial partitioning into two clusters, then repeated splitting of the largest cluster to get additional clusters.
KMeansBisecting.Parameterizer<V extends NumberVector,M extends MeanModel>	Parameterization class.
KMeansCompare<V extends NumberVector>	Compare-Means: Accelerated k-means by exploiting the triangle inequality and pairwise distances of means to prune candidate means.
KMeansCompare.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansElkan<V extends NumberVector>	Elkan's fast k-means by exploiting the triangle inequality.
KMeansElkan.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansHamerly<V extends NumberVector>	Hamerly's fast k-means by exploiting the triangle inequality.
KMeansHamerly.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansHybridLloydMacQueen<V extends NumberVector>	A hybrid k-means algorithm, alternating between MacQueen-style incremental processing and Lloyd-Style batch steps.
KMeansHybridLloydMacQueen.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansLloyd<V extends NumberVector>	The standard k-means algorithm, using Lloyd-style bulk iterations.
KMeansLloyd.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansMacQueen<V extends NumberVector>	The original k-means algorithm, using MacQueen style incremental updates; making this effectively an "online" (streaming) algorithm.
KMeansMacQueen.Parameterizer<V extends NumberVector>	Parameterization class.
KMeansSort<V extends NumberVector>	Sort-Means: Accelerated k-means by exploiting the triangle inequality and pairwise distances of means to prune candidate means (with sorting).
KMeansSort.Parameterizer<V extends NumberVector>	Parameterization class.
KMediansLloyd<V extends NumberVector>	k-medians clustering algorithm, but using Lloyd-style bulk iterations instead of the more complicated approach suggested by Kaufman and Rousseeuw (see KMedoidsPAM instead).
KMediansLloyd.Parameterizer<V extends NumberVector>	Parameterization class.
KMedoidsEM<V>	A k-medoids clustering algorithm, implemented as EM-style bulk algorithm.
KMedoidsEM.Parameterizer<V>	Parameterization class.
KMedoidsPAM<V>	The original PAM algorithm or k-medoids clustering, as proposed by Kaufman and Rousseeuw in "Partitioning Around Medoids".
KMedoidsPAM.Parameterizer<V>	Parameterization class.
SingleAssignmentKMeans<V extends NumberVector>	Pseudo-k-Means variations, that assigns each object to the nearest center.
SingleAssignmentKMeans.Parameterizer<V extends NumberVector>	Parameterization class.
XMeans<V extends NumberVector,M extends MeanModel>	X-means: Extending K-means with Efficient Estimation on the Number of Clusters.
XMeans.Parameterizer<V extends NumberVector,M extends MeanModel>	Parameterization class.

Package de.lmu.ifi.dbs.elki.algorithm.clustering.kmeans Description

K-means clustering and variations.