Matrix (ELKI: Environment for DeveLoping KDD-Applications Supported by Index-Structures)

java.lang.Object
- de.lmu.ifi.dbs.elki.math.linearalgebra.Matrix

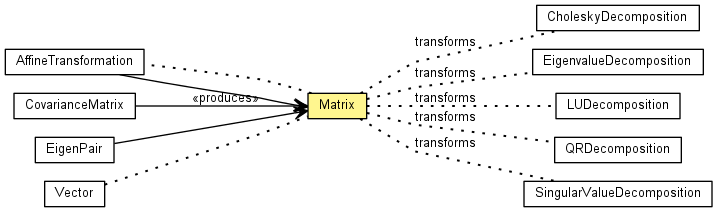
```
public class Matrix
extends Object
```
A two-dimensional matrix class, where the data is stored as two-dimensional array. Implementation note: this class contains various optimizations that theoretically the java hotspot compiler should optimize on its own. However, they do show up a hotspots in the profiler (in cpu=times mode), so it does make a difference at least when optimizing other parts of ELKI.

Author:

Elke Achtert, Erich Schubert

Field Summary

Fields
Modifier and Type	Field and Description
`(package private) int`	`columndimension` Column dimension.
`static double`	`DELTA` A small number to handle numbers near 0 as 0.
`protected double[][]`	`elements` Array for internal storage of elements.
`static String`	`ERR_MATRIX_DIMENSIONS` Error when matrix dimensions do not agree.
`private static String`	`ERR_MATRIX_INNERDIM` Error when matrix inner dimensions do not agree.
`static String`	`ERR_NOTRECTANGULAR` Error: matrix not rectangular.
`static String`	`ERR_REINDEX` Error: matrix indexes incorrect
`static double`	`SINGULARITY_CHEAT` Small value to increment diagonally of a matrix in order to avoid singularity before building the inverse.

Constructor Summary

Constructors
Constructor and Description
`Matrix(double[][] elements)` Constructs a matrix from a 2-D array.
`Matrix(double[] values, int m)` Construct a matrix from a one-dimensional packed array
`Matrix(int m, int n)` Constructs an m-by-n matrix of zeros.
`Matrix(int m, int n, double s)` Constructs an m-by-n constant matrix.
`Matrix(Matrix mat)` Constructor, cloning an existing matrix.

Method Summary

Methods
Modifier and Type	Method and Description
`boolean`	`almostEquals(Object obj)` Compare two matrices with a delta parameter to take numerical errors into account.
`boolean`	`almostEquals(Object obj, double maxdelta)` Compare two matrices with a delta parameter to take numerical errors into account.
`Matrix`	`appendColumns(Matrix columns)` Returns a matrix which consists of this matrix and the specified columns.
`Matrix`	`cheatToAvoidSingularity(double constant)` Adds a given value to the diagonal entries if the entry is smaller than the constant.
`protected void`	`checkMatrixDimensions(Matrix B)` Check if size(A) == size(B)
`Matrix`	`clone()` Clone the Matrix object.
`Matrix`	`completeBasis()` Completes this d x c basis of a subspace of R^d to a d x d basis of R^d, i.e. appends c-d columns to this basis.
`Matrix`	`completeToOrthonormalBasis()` Completes this d x c basis of a subspace of R^d to a d x d basis of R^d, i.e. appends c-d columns to this basis.
`double`	`cond()` Matrix condition (2 norm)
`static Matrix`	`constructWithCopy(double[][] A)` Construct a matrix from a copy of a 2-D array.
`Matrix`	`copy()` Make a deep copy of a matrix.
`double`	`det()` Matrix determinant
`static Matrix`	`diagonal(double[] diagonal)` Returns a quadratic Matrix consisting of zeros and of the given values on the diagonal.
`static Matrix`	`diagonal(Vector diagonal)` Returns a quadratic Matrix consisting of zeros and of the given values on the diagonal.
`boolean`	`equals(Object obj)`
`double`	`get(int i, int j)` Get a single element.
`double[][]`	`getArrayCopy()` Copy the internal two-dimensional array.
`double[][]`	`getArrayRef()` Access the internal two-dimensional array.
`Vector`	`getCol(int j)` Returns the `j`th column of this matrix as vector.
`int`	`getColumnDimensionality()` Returns the dimensionality of the columns of this matrix.
`double[]`	`getColumnPackedCopy()` Make a one-dimensional column packed copy of the internal array.
`Matrix`	`getMatrix(int[] r, int[] c)` Get a submatrix.
`Matrix`	`getMatrix(int[] r, int j0, int j1)` Get a submatrix.
`Matrix`	`getMatrix(int i0, int i1, int[] c)` Get a submatrix.
`Matrix`	`getMatrix(int i0, int i1, int j0, int j1)` Get a submatrix.
`Vector`	`getRow(int i)` Returns the `i`th row of this matrix as vector.
`int`	`getRowDimensionality()` Returns the dimensionality of the rows of this matrix.
`double[]`	`getRowPackedCopy()` Make a one-dimensional row packed copy of the internal array.
`int`	`hashCode()`
`static Matrix`	`identity(int m, int n)` Generate identity matrix
`Matrix`	`increment(int i, int j, double s)` Increments a single element.
`Matrix`	`inverse()` Matrix inverse or pseudoinverse
`boolean`	`isSymmetric()` Returns true, if this matrix is symmetric, false otherwise.
`boolean`	`linearlyIndependent(Matrix columnMatrix)` Returns true if the specified column matrix `a` is linearly independent to the columns of this matrix.
`Matrix`	`minus(Matrix B)` C = A - B
`Matrix`	`minusEquals(Matrix B)` A = A - B
`Matrix`	`minusTimes(Matrix B, double s)` C = A - s * B
`Matrix`	`minusTimesEquals(Matrix B, double s)` A = A - s * B
`double`	`norm1()` One norm
`double`	`norm2()` Two norm
`void`	`normalizeColumns()` Normalizes the columns of this matrix to length of 1.0.
`double`	`normF()` Frobenius norm
`double`	`normInf()` Infinity norm
`Matrix`	`orthonormalize()` Returns an orthonormalization of this matrix.
`Matrix`	`plus(double s)` C = A + s
`Matrix`	`plus(Matrix B)` C = A + B
`Matrix`	`plusDiagonal(double s)` C = A + s
`Matrix`	`plusDiagonalEquals(double s)` A = A + s
`Matrix`	`plusEquals(double s)` A = A + s
`Matrix`	`plusEquals(Matrix B)` A = A + B
`Matrix`	`plusTimes(Matrix B, double s)` C = A + s * B
`Matrix`	`plusTimesEquals(Matrix B, double s)` A = A + s * B
`static Matrix`	`random(int m, int n)` Generate matrix with random elements
`int`	`rank()` Matrix rank
`static Matrix`	`read(BufferedReader input)` Read a matrix from a stream.
`Matrix`	`robustInverse()` Matrix inverse for square matrixes.
`Matrix`	`set(int i, int j, double s)` Set a single element.
`void`	`setCol(int j, Vector column)` Sets the `j`th column of this matrix to the specified column.
`void`	`setMatrix(int[] r, int[] c, Matrix X)` Set a submatrix.
`void`	`setMatrix(int[] r, int j0, int j1, Matrix X)` Set a submatrix.
`void`	`setMatrix(int i0, int i1, int[] c, Matrix X)` Set a submatrix.
`void`	`setMatrix(int i0, int i1, int j0, int j1, Matrix X)` Set a submatrix.
`void`	`setRow(int j, Vector row)` Sets the `j`th row of this matrix to the specified vector.
`Matrix`	`solve(Matrix B)` Solve A*X = B
`Matrix`	`times(double s)` Multiply a matrix by a scalar, C = s*A
`Matrix`	`times(Matrix B)` Linear algebraic matrix multiplication, A * B
`Vector`	`times(Vector B)` Linear algebraic matrix multiplication, A * B
`Matrix`	`timesEquals(double s)` Multiply a matrix by a scalar in place, A = s*A
`Matrix`	`timesTranspose(Matrix B)` Linear algebraic matrix multiplication, A * B^T
`String`	`toString()` toString returns String-representation of Matrix.
`double`	`trace()` Matrix trace.
`Matrix`	`transpose()` Matrix transpose.
`Matrix`	`transposeTimes(Matrix B)` Linear algebraic matrix multiplication, A^T * B
`Vector`	`transposeTimes(Vector B)` Linear algebraic matrix multiplication, A^T * B
`Matrix`	`transposeTimesTranspose(Matrix B)` Linear algebraic matrix multiplication, A^T * B^T.
`static Matrix`	`unitMatrix(int dim)` Returns the unit matrix of the specified dimension.
`static Matrix`	`zeroMatrix(int dim)` Returns the zero matrix of the specified dimension.

Methods inherited from class java.lang.Object
finalize, getClass, notify, notifyAll, wait, wait, wait

- Field Detail
  - DELTA
```
public static final double DELTA
```
    A small number to handle numbers near 0 as 0.
    
    See Also:
    Constant Field Values
  - SINGULARITY_CHEAT
```
public static final double SINGULARITY_CHEAT
```
    Small value to increment diagonally of a matrix in order to avoid singularity before building the inverse.
    
    See Also:
    Constant Field Values
  - ERR_NOTRECTANGULAR
```
public static final String ERR_NOTRECTANGULAR
```
    Error: matrix not rectangular.
    
    See Also:
    Constant Field Values
  - ERR_REINDEX
```
public static final String ERR_REINDEX
```
    Error: matrix indexes incorrect
    
    See Also:
    Constant Field Values
  - ERR_MATRIX_DIMENSIONS
```
public static final String ERR_MATRIX_DIMENSIONS
```
    Error when matrix dimensions do not agree.
    
    See Also:
    Constant Field Values
  - ERR_MATRIX_INNERDIM
```
private static final String ERR_MATRIX_INNERDIM
```
    Error when matrix inner dimensions do not agree.
    
    See Also:
    Constant Field Values
  - elements
```
protected final double[][] elements
```
    Array for internal storage of elements.
  - columndimension
```
final int columndimension
```
    Column dimension.
- Constructor Detail
  - Matrix
```
public Matrix(int m,
      int n)
```
    Constructs an m-by-n matrix of zeros.
    
    Parameters:
    m - number of rows
    n - number of columns
  - Matrix
```
public Matrix(int m,
      int n,
      double s)
```
    Constructs an m-by-n constant matrix.
    
    Parameters:
    m - number of rows
    n - number of columns
    s - A scalar value defining the constant value in the matrix
  - Matrix
```
public Matrix(double[][] elements)
```
    Constructs a matrix from a 2-D array.
    
    Parameters:
    elements - an array of arrays of doubles defining the values of the matrix
    
    Throws:
    
    IllegalArgumentException - if not all rows conform in the same length
  - Matrix
```
public Matrix(double[] values,
      int m)
```
    Construct a matrix from a one-dimensional packed array
    
    Parameters:
    values - One-dimensional array of doubles, packed by columns (ala Fortran).
    m - Number of rows.
    
    Throws:
    
    IllegalArgumentException - Array length must be a multiple of m.
  - Matrix
```
public Matrix(Matrix mat)
```
    Constructor, cloning an existing matrix.
    
    Parameters:
    mat - Matrix to clone
- Method Detail
  - constructWithCopy
```
public static final Matrix constructWithCopy(double[][] A)
```
    Construct a matrix from a copy of a 2-D array.
    
    Parameters:
    A - Two-dimensional array of doubles.
    
    Returns:
    new matrix
    
    Throws:
    
    IllegalArgumentException - All rows must have the same length
  - unitMatrix
```
public static final Matrix unitMatrix(int dim)
```
    Returns the unit matrix of the specified dimension.
    
    Parameters:
    dim - the dimensionality of the unit matrix
    
    Returns:
    the unit matrix of the specified dimension
  - zeroMatrix
```
public static final Matrix zeroMatrix(int dim)
```
    Returns the zero matrix of the specified dimension.
    
    Parameters:
    dim - the dimensionality of the unit matrix
    
    Returns:
    the zero matrix of the specified dimension
  - random
```
public static final Matrix random(int m,
            int n)
```
    Generate matrix with random elements
    
    Parameters:
    m - Number of rows.
    n - Number of columns.
    
    Returns:
    An m-by-n matrix with uniformly distributed random elements.
  - identity
```
public static final Matrix identity(int m,
              int n)
```
    Generate identity matrix
    
    Parameters:
    m - Number of rows.
    n - Number of columns.
    
    Returns:
    An m-by-n matrix with ones on the diagonal and zeros elsewhere.
  - diagonal
```
public static final Matrix diagonal(double[] diagonal)
```
    Returns a quadratic Matrix consisting of zeros and of the given values on the diagonal.
    
    Parameters:
    diagonal - the values on the diagonal
    
    Returns:
    the resulting matrix
  - diagonal
```
public static final Matrix diagonal(Vector diagonal)
```
    Returns a quadratic Matrix consisting of zeros and of the given values on the diagonal.
    
    Parameters:
    diagonal - the values on the diagonal
    
    Returns:
    the resulting matrix
  - copy
```
public final Matrix copy()
```
    Make a deep copy of a matrix.
    
    Returns:
    a new matrix containing the same values as this matrix
  - clone
```
public Matrix clone()
```
    Clone the Matrix object.
    
    Overrides:
    
    clone in class Object
  - getArrayRef
```
public final double[][] getArrayRef()
```
    Access the internal two-dimensional array.
    
    Returns:
    Pointer to the two-dimensional array of matrix elements.
  - getArrayCopy
```
public final double[][] getArrayCopy()
```
    Copy the internal two-dimensional array.
    
    Returns:
    Two-dimensional array copy of matrix elements.
  - getRowDimensionality
```
public final int getRowDimensionality()
```
    Returns the dimensionality of the rows of this matrix.
    
    Returns:
    m, the number of rows.
  - getColumnDimensionality
```
public final int getColumnDimensionality()
```
    Returns the dimensionality of the columns of this matrix.
    
    Returns:
    n, the number of columns.
  - get
```
public final double get(int i,
         int j)
```
    Get a single element.
    
    Parameters:
    i - Row index.
    j - Column index.
    
    Returns:
    A(i,j)
    
    Throws:
    
    ArrayIndexOutOfBoundsException - on bounds error
  - set
```
public final Matrix set(int i,
         int j,
         double s)
```
    Set a single element.
    
    Parameters:
    i - Row index.
    j - Column index.
    s - A(i,j).
    
    Returns:
    modified matrix
    
    Throws:
    
    ArrayIndexOutOfBoundsException - on bounds error
  - increment
```
public final Matrix increment(int i,
               int j,
               double s)
```
    Increments a single element.
    
    Parameters:
    i - the row index
    j - the column index
    s - the increment value: A(i,j) = A(i.j) + s.
    
    Returns:
    modified matrix
    
    Throws:
    
    ArrayIndexOutOfBoundsException - on bounds error
  - getRowPackedCopy
```
public final double[] getRowPackedCopy()
```
    Make a one-dimensional row packed copy of the internal array.
    
    Returns:
    Matrix elements packed in a one-dimensional array by rows.
  - getColumnPackedCopy
```
public final double[] getColumnPackedCopy()
```
    Make a one-dimensional column packed copy of the internal array.
    
    Returns:
    Matrix elements packed in a one-dimensional array by columns.
  - getMatrix
```
public final Matrix getMatrix(int i0,
               int i1,
               int j0,
               int j1)
```
    Get a submatrix.
    
    Parameters:
    i0 - Initial row index
    i1 - Final row index
    j0 - Initial column index
    j1 - Final column index
    
    Returns:
    A(i0:i1,j0:j1)
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - getMatrix
```
public final Matrix getMatrix(int[] r,
               int[] c)
```
    Get a submatrix.
    
    Parameters:
    r - Array of row indices.
    c - Array of column indices.
    
    Returns:
    A(r(:),c(:))
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - getMatrix
```
public final Matrix getMatrix(int[] r,
               int j0,
               int j1)
```
    Get a submatrix.
    
    Parameters:
    r - Array of row indices.
    j0 - Initial column index
    j1 - Final column index
    
    Returns:
    A(r(:),j0:j1)
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - getMatrix
```
public final Matrix getMatrix(int i0,
               int i1,
               int[] c)
```
    Get a submatrix.
    
    Parameters:
    i0 - Initial row index
    i1 - Final row index
    c - Array of column indices.
    
    Returns:
    A(i0:i1,c(:))
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - setMatrix
```
public final void setMatrix(int i0,
             int i1,
             int j0,
             int j1,
             Matrix X)
```
    Set a submatrix.
    
    Parameters:
    i0 - Initial row index
    i1 - Final row index
    j0 - Initial column index
    j1 - Final column index
    X - A(i0:i1,j0:j1)
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - setMatrix
```
public final void setMatrix(int[] r,
             int[] c,
             Matrix X)
```
    Set a submatrix.
    
    Parameters:
    r - Array of row indices.
    c - Array of column indices.
    X - A(r(:),c(:))
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - setMatrix
```
public final void setMatrix(int[] r,
             int j0,
             int j1,
             Matrix X)
```
    Set a submatrix.
    
    Parameters:
    r - Array of row indices.
    j0 - Initial column index
    j1 - Final column index
    X - A(r(:),j0:j1)
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - setMatrix
```
public final void setMatrix(int i0,
             int i1,
             int[] c,
             Matrix X)
```
    Set a submatrix.
    
    Parameters:
    i0 - Initial row index
    i1 - Final row index
    c - Array of column indices.
    X - A(i0:i1,c(:))
    
    Throws:
    
    ArrayIndexOutOfBoundsException - Submatrix indices
  - getRow
```
public final Vector getRow(int i)
```
    Returns the ith row of this matrix as vector.
    
    Parameters:
    i - the index of the row to be returned
    
    Returns:
    the ith row of this matrix
  - setRow
```
public final void setRow(int j,
          Vector row)
```
    Sets the jth row of this matrix to the specified vector.
    
    Parameters:
    j - the index of the column to be set
    row - the value of the column to be set
  - getCol
```
public final Vector getCol(int j)
```
    Returns the jth column of this matrix as vector.
    
    Parameters:
    j - the index of the column to be returned
    
    Returns:
    the jth column of this matrix
  - setCol
```
public final void setCol(int j,
          Vector column)
```
    Sets the jth column of this matrix to the specified column.
    
    Parameters:
    j - the index of the column to be set
    column - the value of the column to be set
  - transpose
```
public final Matrix transpose()
```
    Matrix transpose.
    
    Returns:
    A^T
  - plus
```
public final Matrix plus(Matrix B)
```
    C = A + B
    
    Parameters:
    B - another matrix
    
    Returns:
    A + B in a new Matrix
  - plus
```
public final Matrix plus(double s)
```
    C = A + s
    
    Parameters:
    s - scalar value
    
    Returns:
    A + s in a new Matrix
  - plusDiagonal
```
public final Matrix plusDiagonal(double s)
```
    C = A + s
    
    Parameters:
    s - scalar value
    
    Returns:
    A + s * E in a new Matrix
  - plusTimes
```
public final Matrix plusTimes(Matrix B,
               double s)
```
    C = A + s * B
    
    Parameters:
    B - another matrix
    s - scalar
    
    Returns:
    A + s * B in a new Matrix
  - plusEquals
```
public final Matrix plusEquals(Matrix B)
```
    A = A + B
    
    Parameters:
    B - another matrix
    
    Returns:
    A + B in this Matrix
  - plusEquals
```
public final Matrix plusEquals(double s)
```
    A = A + s
    
    Parameters:
    s - constant to add to every cell
    
    Returns:
    A + s in this Matrix
  - plusDiagonalEquals
```
public final Matrix plusDiagonalEquals(double s)
```
    A = A + s
    
    Parameters:
    s - constant to add to the diagonal
    
    Returns:
    A + s in this Matrix
  - plusTimesEquals
```
public final Matrix plusTimesEquals(Matrix B,
                     double s)
```
    A = A + s * B
    
    Parameters:
    B - another matrix
    s - Scalar
    
    Returns:
    A + s * B in this Matrix
  - minus
```
public final Matrix minus(Matrix B)
```
    C = A - B
    
    Parameters:
    B - another matrix
    
    Returns:
    A - B in a new Matrix
  - minusTimes
```
public final Matrix minusTimes(Matrix B,
                double s)
```
    C = A - s * B
    
    Parameters:
    B - another matrix
    s - Scalar
    
    Returns:
    A - s * B in a new Matrix
  - minusEquals
```
public final Matrix minusEquals(Matrix B)
```
    A = A - B
    
    Parameters:
    B - another matrix
    
    Returns:
    A - B in this Matrix
  - minusTimesEquals
```
public final Matrix minusTimesEquals(Matrix B,
                      double s)
```
    A = A - s * B
    
    Parameters:
    B - another matrix
    s - Scalar
    
    Returns:
    A - s * B in this Matrix
  - times
```
public final Matrix times(double s)
```
    Multiply a matrix by a scalar, C = s*A
    
    Parameters:
    s - scalar
    
    Returns:
    s*A
  - timesEquals
```
public final Matrix timesEquals(double s)
```
    Multiply a matrix by a scalar in place, A = s*A
    
    Parameters:
    s - scalar
    
    Returns:
    replace A by s*A
  - times
```
public final Matrix times(Matrix B)
```
    Linear algebraic matrix multiplication, A * B
    
    Parameters:
    B - another matrix
    
    Returns:
    Matrix product, A * B
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - times
```
public final Vector times(Vector B)
```
    Linear algebraic matrix multiplication, A * B
    
    Parameters:
    B - a vector
    
    Returns:
    Matrix product, A * B
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - transposeTimes
```
public final Vector transposeTimes(Vector B)
```
    Linear algebraic matrix multiplication, A^T * B
    
    Parameters:
    B - another matrix
    
    Returns:
    Matrix product, A^T * B
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - transposeTimes
```
public final Matrix transposeTimes(Matrix B)
```
    Linear algebraic matrix multiplication, A^T * B
    
    Parameters:
    B - another matrix
    
    Returns:
    Matrix product, A^T * B
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - timesTranspose
```
public final Matrix timesTranspose(Matrix B)
```
    Linear algebraic matrix multiplication, A * B^T
    
    Parameters:
    B - another matrix
    
    Returns:
    Matrix product, A * B^T
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - transposeTimesTranspose
```
public final Matrix transposeTimesTranspose(Matrix B)
```
    Linear algebraic matrix multiplication, A^T * B^T. Computed as (B*A)^T
    
    Parameters:
    B - another matrix
    
    Returns:
    Matrix product, A^T * B^T
    
    Throws:
    
    IllegalArgumentException - Matrix inner dimensions must agree.
  - solve
```
public final Matrix solve(Matrix B)
```
    Solve A*X = B
    
    Parameters:
    B - right hand side
    
    Returns:
    solution if A is square, least squares solution otherwise
  - inverse
```
public final Matrix inverse()
```
    Matrix inverse or pseudoinverse
    
    Returns:
    inverse(A) if A is square, pseudoinverse otherwise.
  - robustInverse
```
public final Matrix robustInverse()
```
    Matrix inverse for square matrixes.
    
    Returns:
    inverse(A), or inverse(A + epsilon E) if singular.
  - det
```
public final double det()
```
    Matrix determinant
    
    Returns:
    determinant
  - rank
```
public final int rank()
```
    Matrix rank
    
    Returns:
    effective numerical rank, obtained from SVD.
  - cond
```
public final double cond()
```
    Matrix condition (2 norm)
    
    Returns:
    ratio of largest to smallest singular value.
  - trace
```
public final double trace()
```
    Matrix trace.
    
    Returns:
    sum of the diagonal elements.
  - norm1
```
public final double norm1()
```
    One norm
    
    Returns:
    maximum column sum.
  - norm2
```
public final double norm2()
```
    Two norm
    
    Returns:
    maximum singular value.
  - normInf
```
public final double normInf()
```
    Infinity norm
    
    Returns:
    maximum row sum.
  - normF
```
public final double normF()
```
    Frobenius norm
    
    Returns:
    sqrt of sum of squares of all elements.
  - normalizeColumns
```
public final void normalizeColumns()
```
    Normalizes the columns of this matrix to length of 1.0.
  - linearlyIndependent
```
public final boolean linearlyIndependent(Matrix columnMatrix)
```
    Returns true if the specified column matrix a is linearly independent to the columns of this matrix. Linearly independence is given, if the matrix resulting from appending a to this matrix has full rank.
    
    Parameters:
    columnMatrix - the column matrix to be tested for linear independence
    
    Returns:
    true if the specified column matrix is linearly independent to the columns of this matrix
  - isSymmetric
```
public final boolean isSymmetric()
```
    Returns true, if this matrix is symmetric, false otherwise.
    
    Returns:
    true, if this matrix is symmetric, false otherwise
  - completeBasis
```
public final Matrix completeBasis()
```
    Completes this d x c basis of a subspace of R^d to a d x d basis of R^d, i.e. appends c-d columns to this basis.
    
    Returns:
    the appended columns
  - completeToOrthonormalBasis
```
public final Matrix completeToOrthonormalBasis()
```
    Completes this d x c basis of a subspace of R^d to a d x d basis of R^d, i.e. appends c-d columns to this basis.
    
    Returns:
    the appended columns
  - appendColumns
```
public final Matrix appendColumns(Matrix columns)
```
    Returns a matrix which consists of this matrix and the specified columns.
    
    Parameters:
    columns - the columns to be appended
    
    Returns:
    the new matrix with the appended columns
  - orthonormalize
```
public final Matrix orthonormalize()
```
    Returns an orthonormalization of this matrix.
    
    Returns:
    the orthonormalized matrix
  - cheatToAvoidSingularity
```
public final Matrix cheatToAvoidSingularity(double constant)
```
    Adds a given value to the diagonal entries if the entry is smaller than the constant.
    
    Parameters:
    constant - value to add to the diagonal entries
    
    Returns:
    a new Matrix differing from this Matrix by the given value added to the diagonal entries
  - read
```
public static final Matrix read(BufferedReader input)
                         throws IOException
```
    Read a matrix from a stream. The format is the same the print method, so printed matrices can be read back in (provided they were printed using US Locale). Elements are separated by whitespace, all the elements for each row appear on a single line, the last row is followed by a blank line.
    
    Parameters:
    input - the input stream.
    
    Returns:
    New matrix
    
    Throws:
    
    IOException - on input error
  - checkMatrixDimensions
```
protected void checkMatrixDimensions(Matrix B)
```
    Check if size(A) == size(B)
  - hashCode
```
public int hashCode()
```
    Overrides:
    
    hashCode in class Object
  - equals
```
public boolean equals(Object obj)
```
    Overrides:
    
    equals in class Object
  - almostEquals
```
public boolean almostEquals(Object obj,
                   double maxdelta)
```
    Compare two matrices with a delta parameter to take numerical errors into account.
    
    Parameters:
    obj - other object to compare with
    maxdelta - maximum delta allowed
    
    Returns:
    true if delta smaller than maximum
  - almostEquals
```
public boolean almostEquals(Object obj)
```
    Compare two matrices with a delta parameter to take numerical errors into account.
    
    Parameters:
    obj - other object to compare with
    
    Returns:
    almost equals with delta DELTA
  - toString
```
public String toString()
```
    toString returns String-representation of Matrix.
    
    Overrides:
    
    toString in class Object

Class Matrix

Field Summary

Constructor Summary

Method Summary

Methods inherited from class java.lang.Object

Field Detail

DELTA

SINGULARITY_CHEAT

ERR_NOTRECTANGULAR

ERR_REINDEX

ERR_MATRIX_DIMENSIONS

ERR_MATRIX_INNERDIM

elements

columndimension

Constructor Detail

Matrix

Matrix

Matrix

Matrix

Matrix

Method Detail

constructWithCopy

unitMatrix

zeroMatrix

random

identity

diagonal

diagonal

copy

clone

getArrayRef

getArrayCopy

getRowDimensionality

getColumnDimensionality

get

set

increment

getRowPackedCopy

getColumnPackedCopy

getMatrix

getMatrix

getMatrix

getMatrix

setMatrix

setMatrix

setMatrix

setMatrix

getRow

setRow

getCol

setCol

transpose

plus

plus

plusDiagonal

plusTimes

plusEquals

plusEquals

plusDiagonalEquals

plusTimesEquals

minus

minusTimes

minusEquals

minusTimesEquals

times

timesEquals

times

times

transposeTimes

transposeTimes

timesTranspose

transposeTimesTranspose

solve

inverse

robustInverse

det

rank

cond

trace

norm1