Package de.lmu.ifi.dbs.elki.math.linearalgebra

Linear Algebra package provides classes and computational methods for operations on matrices.

See:
Description

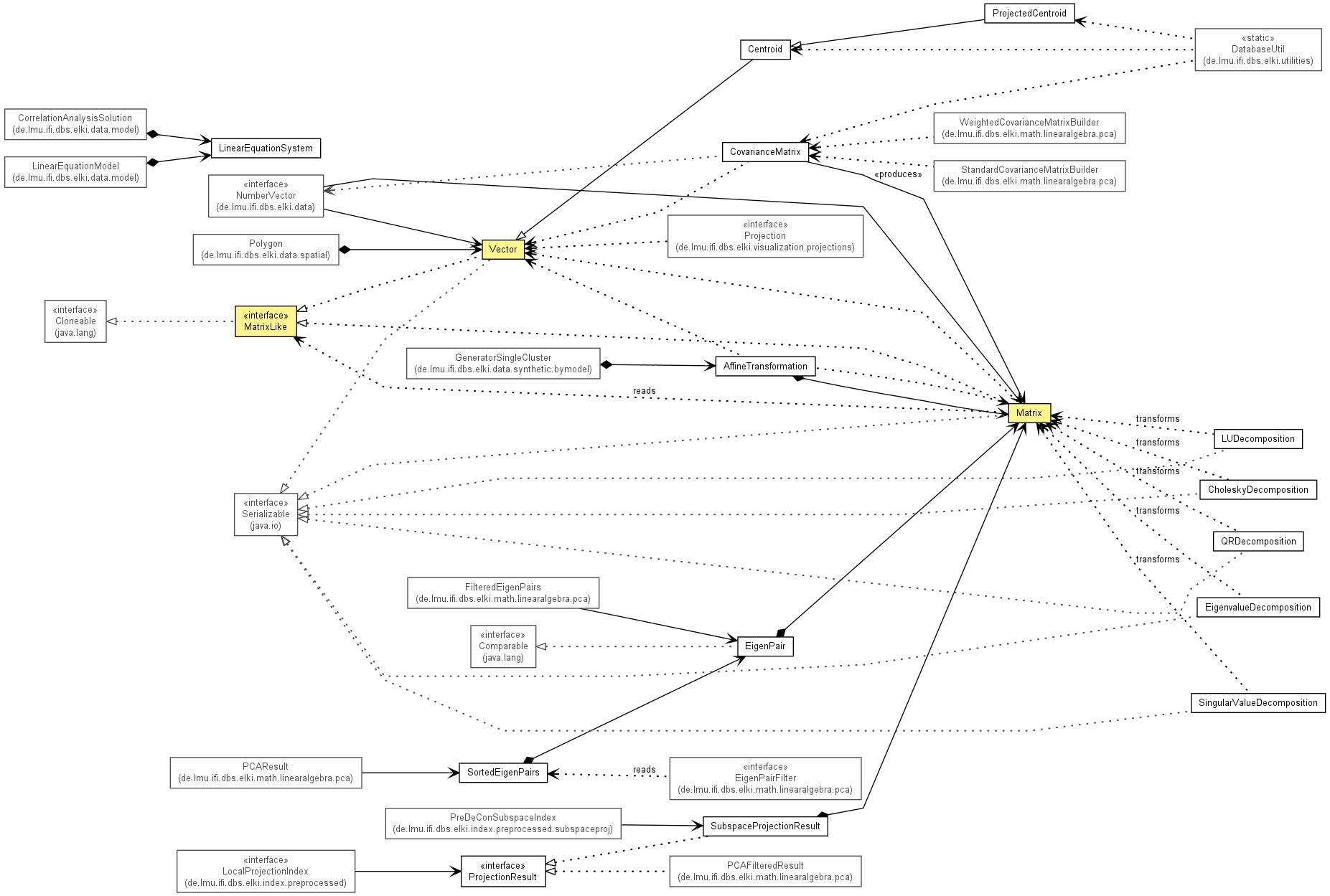
Interface Summary

MatrixLike<M extends MatrixLike<M>>	Common Interface for Matrix and Vector objects, where M is the actual type.
ProjectionResult	Interface representing a simple projection result.

Class Summary

AffineTransformation	Affine transformations implemented using homogeneous coordinates.
Centroid	Class to compute the centroid of some data.
CholeskyDecomposition	Cholesky Decomposition.
CovarianceMatrix	Class for computing covariance matrixes using stable mean and variance computations.
EigenPair	Helper class which encapsulates an eigenvector and its corresponding eigenvalue.
EigenvalueDecomposition	Eigenvalues and eigenvectors of a real matrix.
LinearEquationSystem	Class for systems of linear equations.
LUDecomposition	LU Decomposition.
Matrix	A two-dimensional matrix class, where the data is stored as two-dimensional array.
ProjectedCentroid	Centroid only using a subset of dimensions.
QRDecomposition	QR Decomposition.
SingularValueDecomposition	Singular Value Decomposition.
SortedEigenPairs	Helper class which encapsulates an array of eigenpairs (i.e. an array of eigenvectors and their corresponding eigenvalues).
SubspaceProjectionResult	Simple class wrapping the result of a subspace projection.
Vector	Provides a vector object that encapsulates an m x 1 - matrix object.

Package de.lmu.ifi.dbs.elki.math.linearalgebra Description

Linear Algebra package provides classes and computational methods for operations on matrices.

The content of this package is adapted from the Jama package.

Five fundamental matrix decompositions, which consist of pairs or triples of matrices, permutation vectors, and the like, produce results in five decomposition classes. These decompositions are accessed by the Matrix class to compute solutions of simultaneous linear equations, determinants, inverses and other matrix functions. The five decompositions are:

• Cholesky Decomposition of symmetric, positive definite matrices.
• LU Decomposition of rectangular matrices.
• QR Decomposition of rectangular matrices.
• Singular Value Decomposition of rectangular matrices.
• Eigenvalue Decomposition of both symmetric and nonsymmetric square matrices.

Example of use:

Solve a linear system A x = b and compute the residual norm, ||b - A x||.

      double[][] vals = {{1.,2.,3},{4.,5.,6.},{7.,8.,10.}};
      Matrix A = new Matrix(vals);
      Matrix b = Matrix.random(3,1);
      Matrix x = A.solve(b);
      Matrix r = A.times(x).minus(b);
      double rnorm = r.normInf();

The original Jama-package has been developed by the MathWorks and NIST and can be found at http://math.nist.gov/javanumerics/jama/. Here, for the adaption some classes and methods convenient for data mining applications within ELKI were added. Furthermore some erroneous comments were corrected and the coding-style was subtly changed to a more Java-typical style.