- Overview
- Package
- Class
- Use
- Tree
- Deprecated
- Index

See: Description
| Interface | Description |
|---|---|
| CovarianceMatrixBuilder |
Interface for computing covariance matrixes on a data set.
|
| EigenPairFilter |
The eigenpair filter is used to filter eigenpairs (i.e. eigenvectors
and their corresponding eigenvalues) which are a result of a
Variance Analysis Algorithm, e.g.
|
| Class | Description |
|---|---|
| AbstractCovarianceMatrixBuilder |
Abstract class with the task of computing a Covariance matrix to be used in PCA.
|
| CompositeEigenPairFilter |
The
CompositeEigenPairFilter can be used to build a chain of
eigenpair filters. |
| CompositeEigenPairFilter.Parameterizer |
Parameterization class.
|
| DropEigenPairFilter |
The "drop" filter looks for the largest drop in normalized relative
eigenvalues.
|
| DropEigenPairFilter.Parameterizer |
Parameterization class.
|
| FilteredEigenPairs |
Encapsulates weak and strong eigenpairs that have been filtered out
by an eigenpair filter.
|
| FirstNEigenPairFilter |
The FirstNEigenPairFilter marks the n highest eigenpairs as strong
eigenpairs, where n is a user specified number.
|
| FirstNEigenPairFilter.Parameterizer |
Parameterization class.
|
| LimitEigenPairFilter |
The LimitEigenPairFilter marks all eigenpairs having an (absolute) eigenvalue
below the specified threshold (relative or absolute) as weak eigenpairs, the
others are marked as strong eigenpairs.
|
| LimitEigenPairFilter.Parameterizer |
Parameterization class.
|
| NormalizingEigenPairFilter |
The NormalizingEigenPairFilter normalizes all eigenvectors s.t.
|
| PCAFilteredAutotuningRunner |
Performs a self-tuning local PCA based on the covariance matrices of given
objects.
|
| PCAFilteredAutotuningRunner.Cand |
Candidate
|
| PCAFilteredAutotuningRunner.Parameterizer |
Parameterization class.
|
| PCAFilteredResult |
Result class for a filtered PCA.
|
| PCAFilteredRunner |
PCA runner that will do dimensionality reduction.
|
| PCAFilteredRunner.Parameterizer |
Parameterization class.
|
| PCAResult |
Result class for Principal Component Analysis with some convenience methods
|
| PCARunner |
Class to run PCA on given data.
|
| PCARunner.Parameterizer |
Parameterization class.
|
| PercentageEigenPairFilter |
The PercentageEigenPairFilter sorts the eigenpairs in descending order of
their eigenvalues and marks the first eigenpairs, whose sum of eigenvalues is
higher than the given percentage of the sum of all eigenvalues as strong
eigenpairs.
|
| PercentageEigenPairFilter.Parameterizer |
Parameterization class.
|
| ProgressiveEigenPairFilter |
The ProgressiveEigenPairFilter sorts the eigenpairs in descending order of
their eigenvalues and marks the first eigenpairs, whose sum of eigenvalues is
higher than the given percentage of the sum of all eigenvalues as strong
eigenpairs.
|
| ProgressiveEigenPairFilter.Parameterizer |
Parameterization class.
|
| RANSACCovarianceMatrixBuilder |
RANSAC based approach to a more robust covariance matrix computation.
|
| RANSACCovarianceMatrixBuilder.Parameterizer |
Parameterization class
|
| RelativeEigenPairFilter |
The RelativeEigenPairFilter sorts the eigenpairs in descending order of their
eigenvalues and marks the first eigenpairs who are a certain factor above the
average of the remaining eigenvalues.
|
| RelativeEigenPairFilter.Parameterizer |
Parameterization class.
|
| SignificantEigenPairFilter |
The SignificantEigenPairFilter sorts the eigenpairs in descending order of
their eigenvalues and chooses the contrast of an Eigenvalue to the remaining
Eigenvalues is maximal.
|
| SignificantEigenPairFilter.Parameterizer |
Parameterization class.
|
| StandardCovarianceMatrixBuilder |
Class for building a "traditional" covariance matrix.
|
| WeakEigenPairFilter |
The WeakEigenPairFilter sorts the eigenpairs in descending order of their
eigenvalues and returns the first eigenpairs who are above the average mark
as "strong", the others as "weak".
|
| WeakEigenPairFilter.Parameterizer |
Parameterization class.
|
| WeightedCovarianceMatrixBuilder |
CovarianceMatrixBuilder with weights. |
| WeightedCovarianceMatrixBuilder.Parameterizer |
Parameterization class.
|
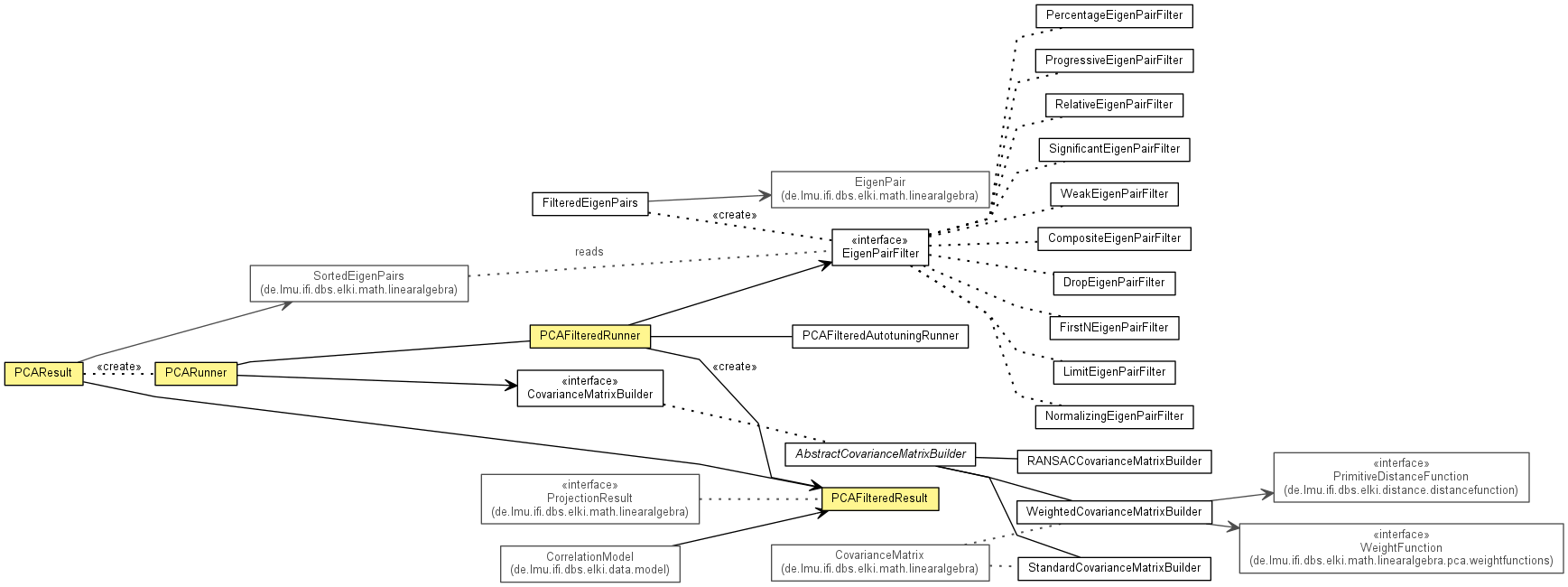
Principal Component Analysis (PCA) and Eigenvector processing.
Copyright © 2015 ELKI Development Team, Lehr- und Forschungseinheit für Datenbanksysteme, Ludwig-Maximilians-Universität München. License information.